Iterated Forcing with Finitely Additive Measures: Applications of Probability to Forcing Theory
(Forcing iterado con medidas finitamente aditivas: aplicaciones de la probabilidad en la teoría del forcing)

El infinito, de la paradoja a la ciencia. Citando una célebre frase de David Hilbert: “Ninguna otra cuestión ha conmovido tan profundamente el espíritu humano; ninguna otra idea ha estimulado tan fecundamente su intelecto; y, sin embargo, ningún otro concepto necesita mayor clarificación que el del infinito”.
El infinito ha sido, desde los albores de la filosofía y la ciencia, un aparente misterio que fascina y desconcierta por igual. Aparece ya insinuado en las paradojas de Zenón de Elea, que cuestionaban la posibilidad misma del movimiento, y se despliega con mayor claridad en la obra de Aristóteles, quien ofreció una clasificación que todavía hoy guía nuestra manera de pensar: el infinito potencial, ese que se construye paso a paso sin alcanzarse nunca por completo—como contar números sin fin—y el infinito actual, concebido como una totalidad ya acabada y presente en sí misma.
Siglos más tarde, Galileo retomó esta inquietud en sus Diálogos sobre dos nuevas ciencias, revelando lo desconcertante de la noción. Señaló que, aunque a primera vista parece haber más números naturales que cuadrados perfectos—pues no todos los números son cuadrados—en realidad ambas colecciones poseen el mismo “tamaño”. La razón es simple pero muy profunda: a cada número natural le corresponde exactamente un cuadrado perfecto. Así, al 1 le corresponde el \(1^2\), al 2 el \(2^2\), al 3 el \(3^2\), al 4 el \(4^2\), y así indefinidamente. Este razonamiento, en apariencia ingenuo, encierra una de las claves más profundas de la matemática moderna: la equipotencia, la idea de que dos conjuntos infinitos pueden ser puestos en correspondencia uno a uno, revelando que “tener el mismo número de elementos” es un concepto mucho más sutil cuando se habla del infinito. Una noción que, lejos de ser un simple juego intelectual, ha transformado radicalmente nuestra comprensión de las matemáticas, del universo, e incluso de los límites del pensamiento humano.
Nuestro trabajo: el desarrollo de una teoría general. Los cardinales pueden clasificarse según un concepto de aproximación llamado cofinalidad, lo que da lugar a dos tipos fundamentales: regulares y singulares, siendo éstos últimos más complejos en general. La cofinalidad mínima que puede tener un cardinal infinito es \(\aleph_0\). A finales de la década de 1980, se sabía que esto no ocurría para los cardinales del diagrama de Cichoń, cuya cofinalidad resultaba siempre mayor a \(\aleph_0\). Sin embargo, existía una excepción: \(\mathrm{cov}(\mathbb{N})\), cuya cofinalidad seguía siendo un problema abierto. En el año 2000, Saharon Shelah—uno de los lógicos más influyentes de la historia de las matemáticas—introdujo un método innovador que combinaba la teoría del forcing de Cohen con ideas de la teoría de la probabilidad, involucrando las llamadas medidas finitamente aditivas y demostrando que, en contraste con lo que se conocía sobre otros cardinales invariantes, \(\mathrm{cov}(\mathbb{N})\) podía, de hecho, tener cofinalidad \(\aleph_0\), un resultado tanto notable como inesperado.
Partiendo de las ideas de Shelah, y de trabajos posteriores de Anda Tanasie y Jakob Kellner—investigadores de la Universidad Tecnológica de Viena—en este proyecto desarrollamos una teoría general de forcing usando medidas finitamente aditivas, la cual permitió generalizar el método de Shelah y establecer un marco común que se ha convertido en una herramienta muy poderosa para abordar problemas de combinatoria de los números reales. Esta teoría se distingue por su marcado carácter interdisciplinario, pues su desarrollo exigió la interacción de ramas en principio alejadas de las matemáticas, como la teoría de conjuntos, la teoría de la probabilidad y el análisis matemático.
En particular, fue necesario elaborar nuevas herramientas en teoría de la probabilidad y en análisis matemático. En el primer caso, propusimos una formalización conjuntista de la noción de árbol de probabilidad y llevamos a cabo un estudio detallado de este tipo de árboles y sus conexiones con medidas de Borel; en el segundo, llevamos a cabo un estudio detallado de medidas finitamente aditivas sobre álgebras Booleanas, entre lo cual se destaca el desarrollo de una teoría de la integración sobre álgebras Booleanas con respecto a medidas finitamente aditivas. Finalmente, aplicamos nuestra teoría para encontrar una nueva configuración del diagrama de Cichoń, donde \(\mathrm{cov}(\mathbb{N})\) puede ser singular y posiblemente de cofinalidad \(\aleph_0\). Este resultado no solo contribuye y amplía nuestro entendimiento sobre la estructura de los números reales, sino que también abre una nueva gama de preguntas sobre la posibilidad de incluir valores singulares en el diagrama, abriendo así caminos inéditos en la investigación de la combinatoria infinita.
Andrés Felipe Uribe Zapata. Estudiante de doctorado de TU Wien, Institute of Discrete Mathematics and Geometry (Viena, Austria) y Diego Alejandro Mejía Guzmán, Profesor Asociado de Kobe University, Graduate School of System Informatics (Kobe, Japón)
Aporte colombiano a la comprensión de los números reales
La matemática suele percibirse como un distante mundo de símbolos y fórmulas, pero es una ciencia cuyo lenguaje abarca tanto las bases teóricas del universo como aspectos esenciales de la vida cotidiana. Por ejemplo, la probabilidad influye en el diseño de seguros y vacunas; la geometría y el álgebra hacen posible el GPS, y la lógica es la base de los algoritmos que guían la inteligencia artificial.
Esta tesis de maestría, laureada por la Universidad Nacional, combina las medidas finitamente aditivas –un concepto de la probabilidad– con la técnica del forcing, formulada en 1963 para abordar cuestiones indecidibles. Estas son las que no pueden resolverse dentro de la teoría de conjuntos, que es el lenguaje sobre el que se sustentan la mayoría de las matemáticas contemporáneas.
El ejemplo más notable de estas cuestiones es la Hipótesis del Continuo –uno de los grandes problemas de la historia de las matemáticas–, relacionada con el tamaño del conjunto de los números reales, es decir, todos aquellos que aparecen en la recta numérica, desde los naturales y las fracciones hasta decimales infinitos (como √2 o π), y que forman una línea sin interrupciones.
La investigación de Andrés Uribe y Diego Mejía sistematiza y amplía ideas planteadas en las últimas dos décadas, que carecían de un marco unificado, y desarrolla una teoría general. Se trata de un avance en el área de las matemáticas puras, no en el de las aplicadas, por lo cual no resuelve un problema de la vida real, al menos por ahora.
Su relevancia se manifiesta en dos aspectos. En primer lugar, la nueva teoría es una herramienta poderosa para abordar problemas de la teoría de conjuntos. Prestigiosas revistas científicas han validado los resultados obtenidos a partir de ella, tanto por los propios autores como por otros investigadores. Además, abre nuevas perspectivas y contribuye a profundizar la comprensión de la estructura de los números reales, uno de los ejes de las matemáticas.
Los límites de las matemáticas y la teoría de forcing. En el siglo XIX, el infinito siguió siendo objeto de profundas reflexiones filosóficas y matemáticas, como se puede apreciar—por ejemplo—en Paradoxes de l’infini de Bernard Bolzano. Sin embargo, no fue hasta la aparición de Georg Cantor, un matemático nacido en San Petersburgo en 1845, que el infinito se convirtió en un objeto plenamente matemático, capaz de conectarse con problemas de distintas ramas de la disciplina. Cantor formalizó la noción del infinito y emprendió un estudio sistemático del mismo, creando una nueva rama de las matemáticas que hoy conocemos como Teoría de Conjuntos. Su objetivo inicial era comprender la naturaleza, el comportamiento y las propiedades del infinito. Para ello, basado en la idea de equipotencia, introdujo el concepto de números cardinales, que extienden la idea de número más allá de los naturales, permitiendo medir y comparar distintos tipos de infinitos. Como resultado de esto, Cantor obtuvo los números álef \((\aleph)\), una jerarquía ordenada que captura todos los infinitos posibles, demostró que el tamaño de los números naturales representa el infinito “más pequeño” posible—el cual se denota como \(\aleph_0\) y resulta ser el primer cardinal de la jerarquía—y también demostró que ésta es no acotada en el sentido de que siempre es posible construir un infinito mayor que cualquier otro infinito dado.
Cantor se interesó de manera particular en el estudio del conjunto de los números reales \(\mathbb{R}\), preguntándose cómo era posible determinar su tamaño dentro de la jerarquía de los álef, logrando demostrar que—en contraste a lo que sucede con los números enteros y racionales—el tamaño de \(\mathbb{R}\) es diferente de \(\aleph_0\). De esta inquietud surgió uno de los problemas más célebres de la historia de las matemáticas: la Hipótesis del Continuo, la cual propone—de manera elemental—que el tamaño de \(\mathbb{R}\), el cual se denota por \(\mathfrak{c}\), corresponde a \(\aleph_1\)—el cardinal que sucede a \(\aleph_0\) en la jerarquía de los infinitos. El estudio de este problema no solo obsesionó a Cantor hasta literalmente conducirlo a la locura, sino que eventualmente reveló un límite sorprendente de las matemáticas: existen problemas independientes, es decir, que no pueden ser demostrados ni refutados. Esto fue producto del trabajo posterior de Paul Cohen, quien en 1963 desarrolló el conocido Método del Forcing para demostrar que la Hipótesis del Continuo es independiente de ZFC—el sistema axiomático en el cual la mayoría de las matemáticas contemporáneas están fundamentadas. Esto puso de manifiesto que la noción de infinito supera nuestras construcciones matemáticas, revelando que incluso la matemática formal tiene límites, transformando para siempre nuestra comprensión de los números y los conjuntos, y redefiniendo los límites del conocimiento humano.
Los números reales y su estructura. Cantor murió sin saber que la Hipótesis del Continuo no podía resolverse, no sin antes haber realizado numerosos intentos infructuosos de probarla o refutarla. Sin embargo, estos esfuerzos no fueron en vano, ya que resultaron ser fundamentales en nuestra compresión de la estructura de los números reales, al obtener nuevos teoremas y desarrollar herramientas capaces de abordar problemas combinatorios. Sus investigaciones dieron origen, por ejemplo, a nuevas ramas de las matemáticas, como la Teoría Descriptiva de Conjuntos, o la Combinatoria Infinita—marco en el cual se desarrolla este proyecto de investigación—que permite estudiar la estructura de los reales mediante los llamados cardinales invariantes del continuo. Estos capturan propiedades puramente combinatorias de \(\mathbb{R}\). Por ejemplo, al dotarlos con la Medida de Lebesgue y considerarlo como un espacio de medida, obtenemos la noción de conjunto nulo, un concepto analítico que intuitivamente captura el hecho de que un subconjunto de \(\mathbb{R}\) es “pequeño” en términos de su medida. Partiendo de esto, surgen preguntas fundamentales tales como:
Las respuestas a estas preguntas se pueden capturar mediante cardinales, denotados como \(\mathrm{cov}(\mathcal{N})\), \(\mathrm{non}(\mathcal{N})\), \(\mathrm{add}(\mathcal{N})\) y \(\mathrm{cof}(\mathcal{N})\), respectivamente. Por ejemplo, \(\mathrm{cov}(\mathcal{N})\) es el mínimo tamaño de una familia de subconjuntos nulos de números reales que cubre a \(\mathbb{R}\). Por resultados básicos de teoría de la medida, se sabe que \(\mathrm{cov}(\mathcal{N})\) está estrictamente por encima de \(\aleph_0\) en la jerarquía de los infinitos y por debajo de \(\mathfrak{c}\); es decir, se satisfacen las desigualdades: \(\aleph_0 < \mathrm{cov}(\mathcal{N}) \leq \mathfrak{c}\), regla que se aplica igualmente a los demás cardinales mencionados anteriormente. Si consideramos a \(\mathbb{R}\) como un espacio topológico, se obtienen nuevos cardinales invariantes que responden a las mismas preguntas, pero reemplazando la noción de conjunto nulo por la de conjunto magro, su equivalente topológico. Así, podemos definir cuatro nuevos cardinales invariantes asociados a la estructura de los números reales: \(\mathrm{cov}(\mathcal{M})\), \(\mathrm{non}(\mathcal{M})\), \(\mathrm{add}(\mathcal{M})\) y \(\mathrm{cof}(\mathcal{M})\). La relación de orden entre estos cardinales se ilustra en el llamado diagrama de Cichoń, uno de los objetos de estudio más importantes de la teoría de conjuntos, ya que proporciona información sobre la estructura combinatoria de \(\mathbb{R}\), y que ha motivado en gran medida la creación de nuevos métodos de forcing:
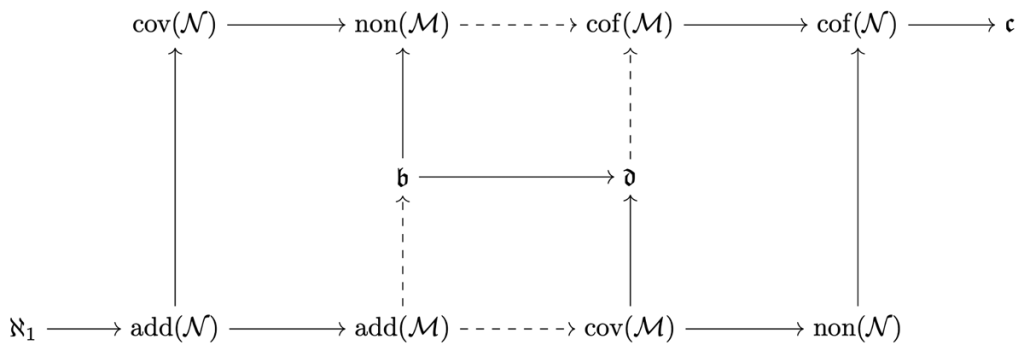
En el diagrama, las flechas significan “menor o igual’’ y las flechas punteadas representan \(\mathrm{add}(\mathcal{M}) = \min\{\mathfrak{b}, \mathrm{cov}(\mathcal{M})\}\) y \(\mathrm{cof}(\mathcal{M}) = \max\{\mathfrak{d}, \mathrm{non}(\mathcal{M})\}\), donde \(\mathfrak{b}\) y \(\mathfrak{d}\) son llamados el número de acotamiento y el número de dominación, respectivamente. Entre 1981 y 1993, un trabajo intenso por parte de Bartoszyński, Cichoń; Fremlin y Pawlikowski; Miller; Raisonnier y Stern; Rothberger y Truss, permitió demostrar las desigualdades fundamentales del diagrama de Cichoń. A su vez, Bartoszyński, Judah, Miller y Shelah completaron el estudio al demostrar que el diagrama es completo, es decir, no es posible añadir más flechas.
Una de las preguntas fundamentales sobre este diagrama y sobre la estructura de \(\mathbb{R}\) era si es posible encontrar configuraciones en las que se pueden separar algunos cardinales, es decir, que tomaran valores diferentes. Por ejemplo, una de estas configuraciones es en la cual todos los cardinales del lado izquierdo tienen valor \(\aleph_1\) y todos los de la derecha tienen valor \(\aleph_2\)—el cardinal que sucede a \(\aleph_1\) en la jerarquía de los infinitos. Este problema permaneció abierto hasta 2021, cuando Martin Goldstern, Jakob Kellner, Diego Mejía y Saharon Shelah construyeron un modelo denominado Cichoń Máximal: una configuración del diagrama en la que todos los cardinales invariantes independientes toman valores distintos. Este resultado puso de manifiesto, de manera concluyente, la extraordinaria complejidad de la estructura de los números reales. Sin embargo, aún quedaban problemas abiertos relacionados con la singularidad de ciertos cardinales, algunos de los cuales fueron abordados en esta investigación.
Al enviar un mensaje a través de WhatsApp, acepta nuestra política de Tratamiento de datos personales
Para información sobre la convocatoria de los Premios de Ciencias y Solidaridad consulte Reglamento, Bases y Requisitos en:
Consultas adicionales las responderemos a partir del 9 de enero de 2025